17世紀位だと微分積分で西洋と日本はほぼ同じレベル
しかし広く公開されていた西洋の数学はさまざまな技術と結びついていったが
日本は「免許」制で流派(関流、建部流、吉田流など)の殻に閉じこもってしまった。
江戸時代には積分はあったけど
微分は無かったんじゃなかったっけ?
関流山路主住の頃には「極限」の論理が確立され、既に微分の方法論も出来ているよ。
有馬頼ゆき(ぎょうにんべんに童)の著述で明らかにされている。
>>8にあるとおり、流派の殻に閉じこもってしまって交流がなかったから。
それをぶった切ろうとした有馬は関流秘伝の数学を全部著述して世間にバラした(拾機算法)
が、影響を考えて豊田文景という偽名で出版している。
有馬頼?(ぎょうにんべんに童)は筑後久留米藩第7代藩主。
新田次郎の「二十一万石の数学者」という小説がある。
微分方程式
これがなかった、というか気づかなかったのが痛い
>>9
なかったようですね
大体フランス語だと20進法みたいな感じで数えるので語呂合わせは不可能でしょう。
他の言語も似たようなもの
どうやら一般人も暗記するという伝統が西洋にはない。
エリート層が聖書を暗記したりはするんだけれども。
東洋は歌で2桁の掛け算を暗記したりする国もあります。
>>10
西洋人は手抜きだからな
しかしその発想がコンピュータを生み出し、またソフトウェアを生み出した。
初の高級プログラム言語「Fortran」を創ったIBMのジョン・バッカ○は、
「メンドーなプログラミングを出来るだけ楽にしたかった」
と明言している。
苦行が美徳とされる東洋からは生まれて来ないんだろうな、こういう技術は
一瞬考え込んでしまたw
そっかー、全体の21/22くらい口開けてんだ(笑)
江戸時代からその萌芽はあったがな
>>28
これだから文系は・・・・・・・・・・・w
西暦年が4で割り切れるが100で割り切れないか
または400で割り切れるのが閏年じゃ
2100年は閏年じゃないぞw
>>30
これだから理系はwwww
そんなもん常識
うるう年の定義の話なんて誰がしているんだ。
歴史的に「4年に1回だった」ことがあると書いたんだ。
現在のようなうるう年になったのは1582年のグレゴリオ13世の暦改定によってだ。
それ以前のユリウス暦は4年に1回だったろwww
ノーベル化学賞受賞の下村博士の研究とはまさにそういうものだった・・・らすぃ
まあ、0の発見(っていうか発明)が紀元600年頃なんだから、近代数学なんてたかだか1500年ぐらいの歴史しかない。
以前なんで0が必要なのか0を見つけるのがなんで難しかったのか考察したことがあるけど、確かに普通じゃ考え付かない(理由と結論が幾重にも交差してるからな)。
ありゃインド人が自慢するのも尤もな気がする。
>>47
0だけじゃだめだね。それじゃ数学理論の基礎の半分でしかない。
もうひとつは「無限」の発見。
これがないと、ささいな算数もその正しさが証明できない。
1/3=0.3333333333333333333333333333333・・・・・・・・・・・・・
が成立するのも、「無限」が前提だからね。
小学生以上は無批判に当たり前だと思っているが。
今力学の統一とか宇宙論の究極が研究されているが、これが正直行き詰っている。
その原因は数学理論が進展しなくなったからだ。
一時期「不確実性の定理」が社会的にも持て囃されたが、それ以来基礎自然科学の分野もほとんど進んでいない。
力学の統一には、10次元ないし11次元の時空間理論が必要だが、数学理論が乏しいのでなかなか進まないんだ。
そろそろピタゴラス、ニュートン、アインシュタインに匹敵する歴史に残る大天才が登場しないと・・・・・・・・・・・。
>>48
不確実性原理が~って、何十年前だよw
ハイゼンベルクのころからしたら量子論なんて飛躍的に進んでるわけだが。
おまい、何かと勘違いしてるんじゃ???
量子論と、数学をゴッチャにしていないかwww
>>58
すまん。そこの後ろは自然科学の話になってたからつい「不確実~」ときいてハイゼンベルクの不確定性原理のことかと早とちりしてしまった。
前の文脈からみればゲーデルの不完全性定理のほうですな。恥さらしてスマソ。
ただ、基礎論のほうの話なら、なおさら自然科学への応用からは離れてしまうような。
たまたま今までは近似計算で形而下(現実)と整合が取れてるように見えたり、公理を拡張して辻褄あわせしてきたけど、
究極だの無限だの元々現実には存在しないものが含まれている体系では、個人的には破綻する気がしている(あくまで個人的には、だぜ)。
まあ、数学を再構築するぐらいの大天才が現れて欲しいのは同感。数学界ってそんなに人材がいないのかね?
>>50
>現実には存在しないものが含まれている体系
ちゃうちゃう。無限というのは「現実の中に存在している」んだよ。
円周率πは無限小数だが、それは円という自然界の中で形成しうるものの中に存在しているんだよ。
「円」自体は抽象の産物だが、その円理論で自然界は成立している。
天体が球状になるのも、水の波紋が円を描くのも。そしてその形状の中に無限小数が介在する自然の法則が内包されている。
それに、
1/3=0.3333333333333333333333333333333・・・・・・・・・・・・・
というのは、それ自体が無限を内在しているだけではなくて、この両辺を3倍した際の整合性の中に無限(この場合正確には極限)の理論が必要になってしまうこと。
算数で両辺を三倍すると、
1=0.9999999999999999999999999999999・・・・・・・・・・・・・・・・・・・・・・・・・
という矛盾が出て、算数は破綻してしまう。
>ちゃうちゃう。無限というのは「現実の中に存在している」んだよ。
残念ながらそれは証明できない。っていうかそれが証明できてたら誰も苦労はしてないだろ?
俺の個人的な見解としては、形而下には無限というものは多分存在しないと思う(ごめん、これも証明はできない)。
確かに「円」というものを想定するのはいいんだけど、現実にあるものはあくまで「近似」として測定されているにすぎないわけでさ。
物理や力学を説明するぐらい範囲の数学だったら公理の拡張ぐらいでなんとかなると思うけど、
元々数学上の要請で必要になった概念が現実と一致するかどうかは誰もわからないわけで。
たまたま今まではそれが運良く一致してきた(ようにみえる)から数学が正しいように見えてるけどさ。
その誤差はどうしても埋まらない気がする。そこを埋めようと躍起になっているわけだけど、
傍からみると「最初の道具立てや仮定がまちがってるんじゃね?」と思う。
まあ俺は数学や物理の専門家じゃないから好きなこといえるんだけど、
「そんなことは分かってる、だからどうしろっていうんだ」っていうのなら謝っておく。
俺にもわからん。
>>52
数学の公理体系と現実が一致する必要はない。現実と一致するかどうかは公理体系のよさとはあまり関係がない。
有用性という面では関係があるかもしれないが、それはたいしたアスペクトじゃない。
適切な数学的議論を取捨選択して現実に応用するのは物理屋の仕事であり、責任。
現実との一致のまずさが問題になるとすれば物理屋の議論が甘いからだよ。
それと近年の基礎物理が停滞っぽく見えるのは、理論がどうこうというより、理論を確かめるための実験ができないことに起因するものの方が大きいのでは?
予算が下りない、技術的に不可能な大きさetcのスペックが必要、とかの理由で。
ひも系もそんな感じ。
日本の場合、流派の数学と世の中の実業がリンクしなかった。
だからそうした要望に応じた形での方法論では後れを取ったな。
暦については進んだが、それも既に西洋に遭ったグレゴリオ暦を
凌駕するようなものは出来なかった。
歴史上の科学者を語ればよい。いろいろ居るではないか。
化学の時間に習う「質量保存の法則」を突き止めた人は、メートル法の制定にも尽力した。
また、酸素の存在を突きとめ、燃焼のメカニズムを解明した。
その人が人生最期に行った実験はたいへん壮絶なものだった。
世界は知らん
しかしそれは技術の歴史だろうな
レーマー(れーまー) Ole Christensen Rmer
(1644―1710)
デンマークの天文学者。木星の衛星の食による光速測定者。
ユトランドの小商家に生まれる。1662年コペンハーゲン大学に入学、複屈折の発見者バルトリンErasmus Bartholin(1625―98)の指示でティコ・ブラーエの手記の編集を任せられた。
71年パリ天文台のJ・ピカールがティコの遺跡を調査に訪れた際にその世話役をつとめて認められ、
72年パリ天文台に招かれた。75年以来木星の衛星の食を観測し続けて、その周期が、衝(しよう)の前後では理論値より約11秒短く、
反対に合(ごう)の前後で約11秒長いことを測定した。
この結果から、光速度は有限であり、地球軌道半径を通過するのに約22分を要するところから、
秒速27万7000キロメートルと定めた。81年母国に帰り母校の数学教授と付置天文台台長を兼任。
天体位置の精密観測のために子午線や赤道儀を考案した。1705年にコペンハーゲン市長、07年に国会議長をも務めた。
http://100.yahoo.co.jp/detail/%E3%AC%E3%BC%E3%9E%E3%BC/
今では考えられないことやオカルトの分野だったことが将来じゃ
科学的に証明されているかもしれないな
最近 占いがオカルトから心理学にうつってるし
昔は催眠術は超魔術だったのに精神分析になってきたし
アインシュタインも最初に絵的な動画直感があってから数式に当てはめていったっていうし
>>101
やはりそうであったか…。アインシュタイン博士…
彼の名言集がある…言葉に感情論がない。まるで何かを悟りきった仙人か神の様に、冷静にかつ的確に物事をスパッと判断している。
超自然主義。
ありのままの様々なこの世に起こりうる現象の本質を見抜いている。言葉に無理がない。
そして…所詮世の中はこんなもんだよ…的な、お爺さんが孫に優しく諭すかの様な、優しい視点。
彼の偉大さは、そんな慈愛に満ちた神的な主観である。
常陸国那珂郡出身で、1663年に全3巻からなる球の体積について記載のある『算爼』を著し、同年に日本で初めて円周率を小数第7桁まで数学的に計算した数学者として知られる。
引用元: ・数学の歴史、科学の歴史
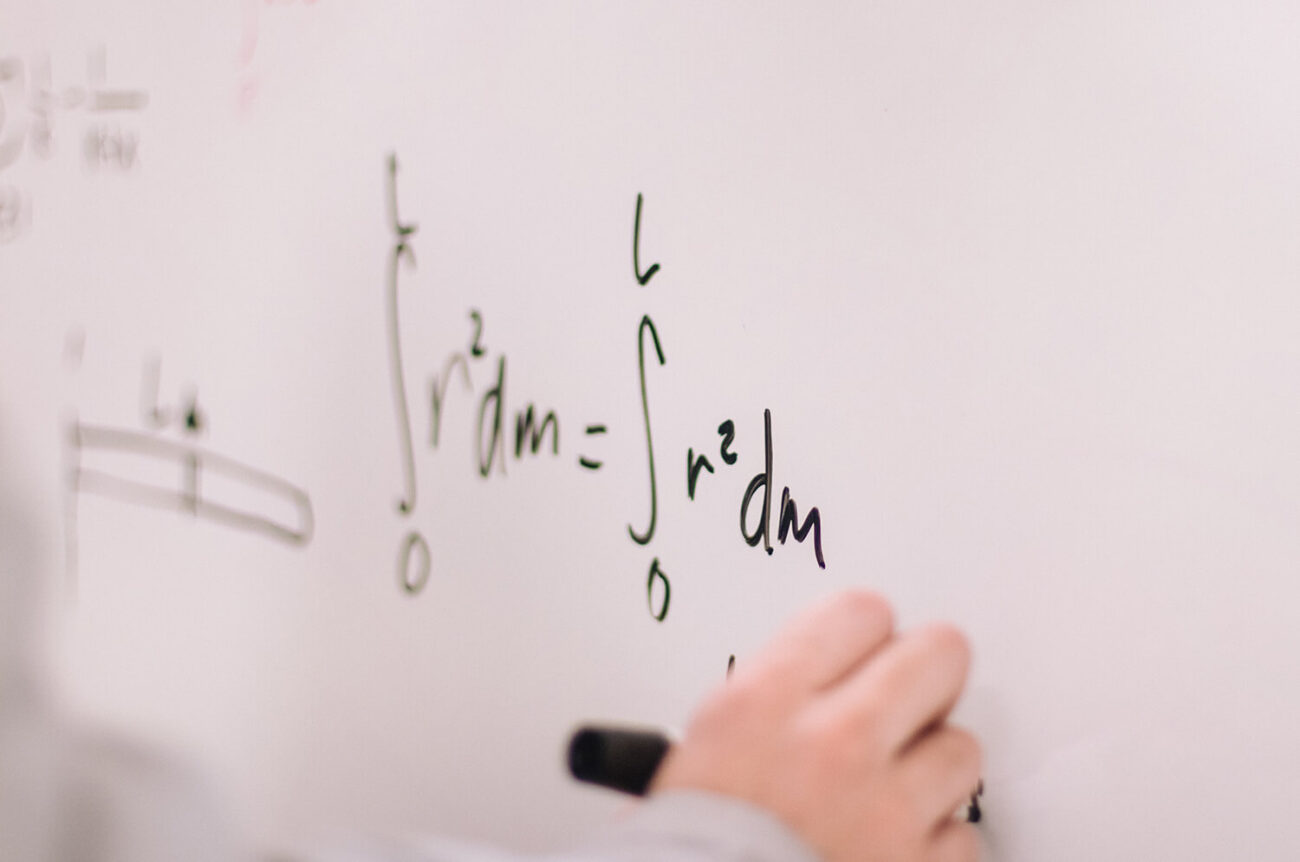
コメント